Predicción de metabolomas ambientales a partir de modelos de flujo metabólico a escala genómica

Gracias a la secuenciación y anotación genómica, en la actualidad es posible conocer los genes presentes en cada organismo y en consecuencia, las posibles reacciones químicas que se pueden encontrar en el genoma. Estas reacciones, por medio de sus sustratos y productos, revelan el perfil metabolómico del organismo en cuestión y a partir de esta información se pueden construir redes que conecten metabolitos y genes a escala genómica.

El movimiento de metabolitos a través de estas redes se ha estudiado por medio del análisis de balance de flujo (FBA por sus siglas en inglés). Este análisis consiste en generar una matriz con la información estequiométrica de todos los metabolitos presentes en el metaboloma (filas) por cada reacción codificada en el genoma (columnas), lo cual limita el hipervolumen metabólico a estados que se podrían encontrar en la célula. A continuación, se define una variable de respuesta que va a ser estimada a partir de la matriz estequiométrica (e.g. crecimiento por producción de macromoléculas), pudiendo modificar la matriz para añadir nutrientes de una fuente externa, por ejemplo glucosa y oxígeno a concentraciones definidas. Además, es posible eliminar enzimas (columnas) de la matriz para simular un fenotipo mutante. De esta manera, fue posible calcular una tasa de crecimiento exponencial para Escherichia coli de 1.65 h-1 con una concentración de glucosa 18.5 mmol, mientras que al eliminar el oxígeno del sistema se obtuvo un crecimiento de 0.47 h-1.

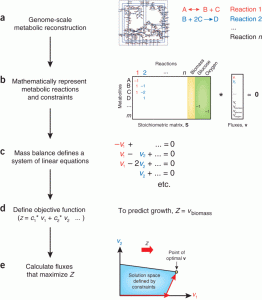
(a) A metabolic network reconstruction consists of a list of stoichiometrically balanced biochemical reactions. (b) This reconstruction is converted into a mathematical model by forming a matrix (labeled S), in which each row represents a metabolite and each column represents a reaction. Growth is incorporated into the reconstruction with a biomass reaction (yellow column), which simulates metabolites consumed during biomass production. Exchange reactions (green columns) are used to represent the flow of metabolites, such as glucose and oxygen, in and out of the cell. (c) At steady state, the flux through each reaction is given by Sv = 0, which defines a system of linear equations. As large models contain more reactions than metabolites, there is more than one possible solution to these equations. (d) Solving the equations to predict the maximum growth rate requires defining an objective function Z = cTv (c is a vector of weights indicating how much each reaction (v) contributes to the objective). In practice, when only one reaction, such as biomass production, is desired for maximization or minimization, c is a vector of zeros with a value of 1 at the position of the reaction of interest. In the growth example, the objective function is Z = vbiomass (that is, c has a value of 1 at the position of the biomass reaction). (e) Linear programming is used to identify a flux distribution that maximizes or minimizes the objective function within the space of allowable fluxes (blue region) defined by the constraints imposed by the mass balance equations and reaction bounds. The thick red arrow indicates the direction of increasing Z. As the optimal solution point lies as far in this direction as possible, the thin red arrows depict the process of linear programming, which identifies an optimal point at an edge or corner of the solution space.

Daniel Garza y compañía escalaron esta metodología y lo aplicaron a comunidades microbianas enteras. Su estrategia, llamada MAMBO, se basa en la idea de que la distribución de abundancias de genomas microbianos y su potencial metabólico refleja la capacidad de los organismos para aprovechar los nutrientes disponibles. Por el método de Monte Carlo para cadenas de Markov, buscaron el ambiente metabólico que produce un crecimiento bacteriano que correlaciona mejor con las abundancias relativas de los genomas observados en datos metagenómicos. Este método fue aplicado para 175 muestras del Proyecto del Microbioma Humano (orales, fecales, vaginales y cutáneos), para lo cual se construyeron modelos metabólicos a escala genómica para 1,562 bacterias detectadas y se encontró una alta correlación entre metabolomas de ambientes similares.

Reference microbial genomes are used to reconstruct GSMMs (1); community abundance profiles are obtained through reference mapping (2); and biomass production of the GSMMs, obtained through FBA (3), is correlated with the metagenomic community abundance profile (4). This correlation is optimized by multiple iterations of a Monte Carlo-based sampling algorithm (5) (see main text and Methods section).

Para comparar su algoritmo con datos experimentales, se utilizaron seis metabolomas anotados de saliva, heces y vagina. Las predicciones de metabolomas orales, fecales y vaginales correlacionaron mejor con sus contrapartes experimentales que con las otras muestras. Finalmente, los autores compararon su estrategia con un algoritmo que predice perfiles metabólicos a partir de la abundancia de genes en los metagenomas y encontraron que MAMBO presenta una mayor consistencia con datos experimentales. Sin embargo, los autores reconocen que este método no toma en cuenta bacteriófagos y factores humanos que podrían influenciar en los metabolomas humanos reales. Además, es poco probable encontrar modelos metabólicos de genomas bacterianos pertenecientes ambientes poco estudiados.

Pearson correlations between 175 metabolomes from four body sites predicted by MAMBo and six experimentally measured metabolomes from literature. Correlations are only shown if > 5 metabolites match between the predicted and measured metabolomes.

Orth, J. D., Thiele, I., & Palsson, B. Ø. (2010). What is flux balance analysis?. Nature biotechnology, 28(3), 245.

Garza, D. R., Verk, M. C., Huynen, M. A., & Dutilh, B. E. (2018). Towards predicting the environmental metabolome from metagenomics with a mechanistic model. Nature microbiology, 1.